Two of our main learning goals for this project include: 1) having clean code and planned out system architecture and 2) learning about how an algorithm works. As such, when we planned out our schedule, we left a lot of time at the beginning of our project for planning and research.

Our main research goal was to figure out what algorithms are typically used to solve the autonomous parallel parking problem and to see if a parallel parking algorithm could be modified to be applied to perpendicular parking. As it turns out, there is a standard calculated path for parallel parking, shown below.

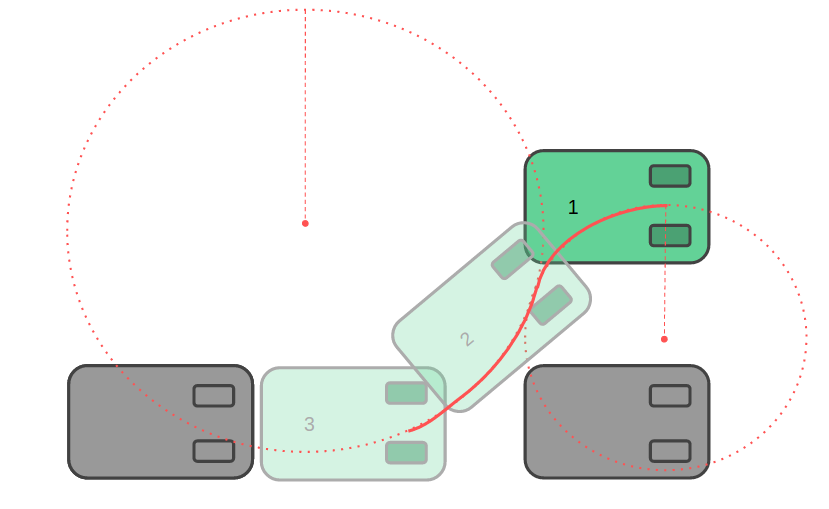
The algorithm works by having the car drive alongside parallel-parked cars while looking for a large enough empty space. Once a space is found, the car drives past the space and aligns itself with the next car. The car then backs into the space, following a path of two tangent semicircle arcs, with origins and radii appropriately calculated to avoid any collisions.

This algorithm immediately had us asking a number of questions, all of which, thankfully, we were able to answer!

1. How will we determine if a spot is empty?

Spot detection can happen in two ways: computer vision analysis or with lidar sensor readings. The computer vision approach would be similar to the method we implemented in our previous project: identifying parking spot delineators, using edge detection to check if the found spot is empty, and applying the pinhole camera model to find the spot’s location relative to the Neato. However, some complications arise when this method is applied to parallel parking. The camera would now have to be on the side of the robot and we might have to deal with stitching multiple images together to create a larger, “panoramic” image that included the entire spot. Scaling the algorithm to work for spot detection on either side of the robot (based on which direction the robot was traveling) would also prove to be more difficult; there would have to be cameras on both sides and a way to determine which camera should be being used. Furthermore, in the real world, not all areas used for parallel parking have spot delineators on the ground, so this method is not general enough to be applicable to actual scenarios.

The lidar implementation, however, solves all of these problems. This method would check the distance readings corresponding to the side of the robot where parking spots are to be expected. If readings are within a certain range, we know that there is a parked car next to our robot (we are assuming the robot will be driving a roughly fixed distance from the parallel spots, just as a car would be doing to stay within its lane). Any readings above that range would signify no car, and thus, an empty spot. Using lidar also simplifies a lot of the calculations and helps us to find parameters of the parking spot with much more ease as we do not have to use the pinhole camera model. For instance, the depth or width of the spot is just the difference between the distance readings of the empty spot and those of a parked car. The length of the spot can be found since we will know how fast the Neato is driving past the spot and the times at which it passes by the edges of the spot. Furthermore, this implementation does not rely on the presence of spot delineators and switching between which side of the car is being checked for spots is simple; the lidar already takes measurements in all 360º.

We were worried that, because the distance between the driving Neato and the parked cars was so small, the lidar readings would be inaccurate or full of noise. However, after testing this implementation by having a Neato drive past “parked” Neatos and an empty spot, we were able to identify clearly the boundaries of an empty spot.

2. How do we get the Neato to traverse a circular path?

When a vehicle drives in a circle, its inner and outer wheels are actually driving in two concentric circles, with the outer wheels driving in the larger circle. For the vehicle to turn properly, the wheels have to be moving along their circles with the same angular velocity, meaning that the outer wheel should be moving with a greater forward velocity to account for the larger distance it needs to travel. Our research on the parallel parking path led us to find that this parking algorithm assumes the vehicle follows the Ackermann Steering Model . Actual cars follow this steering model and turning occurs by having the front inner and outer wheels be offset at different angles to make up for the need for different forward velocities. However, this steering model is definitely not true for a Neato. A Neato, unlike a real car, only has two wheels, which have differential drive. As such, we originally thought we would have to individually control the speeds of each wheel to drive out a desired arc. As we had no experience with such fine control over the Neato, we had no idea of what sorts of complications we might run into with this approach.

However, before looking into this implementation, we realized that our current knowledge of getting a Neato to move involves sending the robot a Twist message through which we set the Neato’s forward and angular velocities. To get the Neato as a whole to drive in an arc, we don’t need to know how the individual wheels are moving. Instead, by simply deciding on a forward velocity v and determining the radius r of the arc based on the size of the parking spot, we can calculate all we need to know in order to send a Twist message. According to the physics of rotational motion, the angular velocity 𝜔 can be found by: 𝜔 = v/r.

We tested this theory and found that, given specific forward and angular velocities, the Neato did indeed traverse a circle with the expected radius. This was a good sign because it signified that error controlling of the Neato’s path would not have to play a large role in our algorithm as wheel slippage did not appear to be a problem.

In our research we also found that the parallel parking path of two tangent arcs can be approximated as part of a cosine. Although we have a working implementation for driving out circular paths, a future feature that we might look into is driving in sinusoidal arcs.

3. Can a similar method be applied to perpendicular parking?

At first, we were doubtful that this circular path parking algorithm could be extended to the perpendicular parking scenario since our previous project had nothing to do with driving in circular paths. However, we were able to find a perpendicular parking algorithm that involves driving past the desired spot and then backing into it in one circular arc.

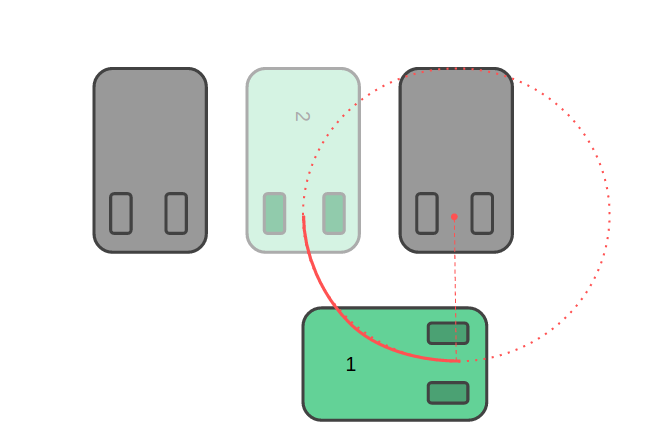
This find meant great news for us! Our perpendicular and parallel algorithms could now be almost identical. By implementing a driveArc(radius) function, both systems could be simplified into a few short steps:

• Determining if the Neato will be driving along parallel or perpendicular parking spaces (either through user input or based on measurements of the spots)
• Drive along parked cars until an empty spot is found, calculating the dimensions of the spot as it is being driven past
• Call the driveArc(radius) function, once for the perpendicular case and twice for the parallel case, where radius is calculated from the parameters of the parking spot

4. Further Considerations

Moving forward, one of the questions we are continuing to consider is how to calculate the origins and radii of the circles. Based on observation, we determined that if the distance between the Neato and the wall is small, then the Neato will drive a minimal distance beyond the next parked car, and the radius of the circle will be fairly small. If the distance between the Neato and the wall is large, then the Neato will drive forward a larger distance, and the radius will be larger. Defining this relationship as a function that determines our origin and radius more precisely is our next step.

Now that we have a solid understanding of how both our parallel and perpendicular parking algorithms will work, as well as thought out plans for our implementation, we are excited to begin implementing and testing!